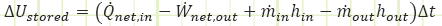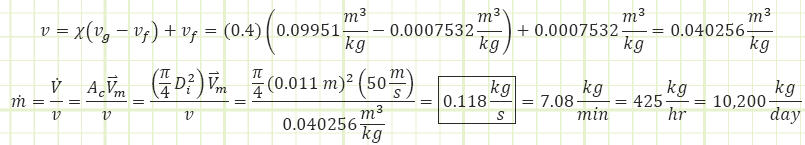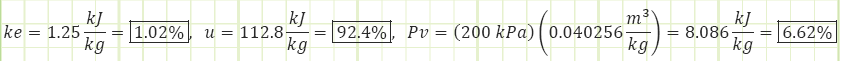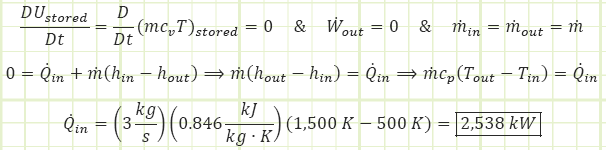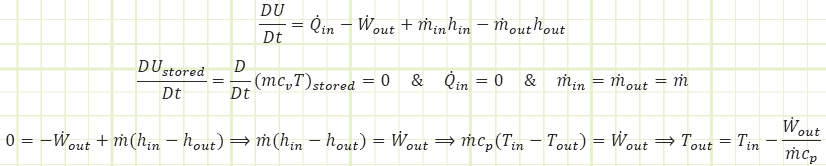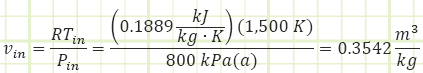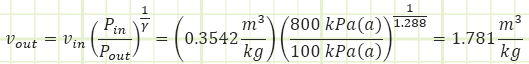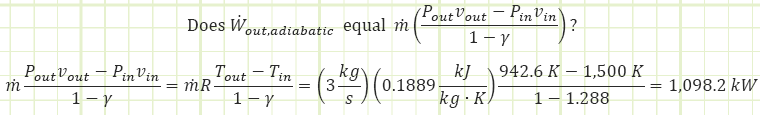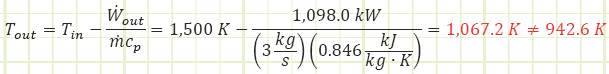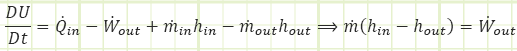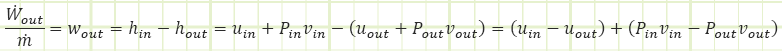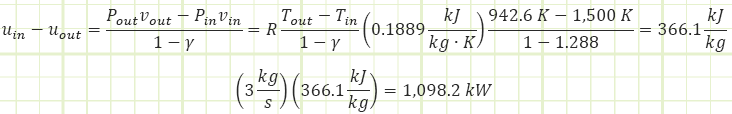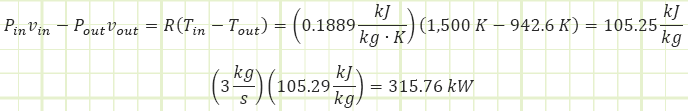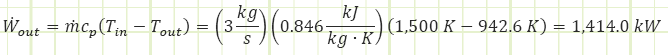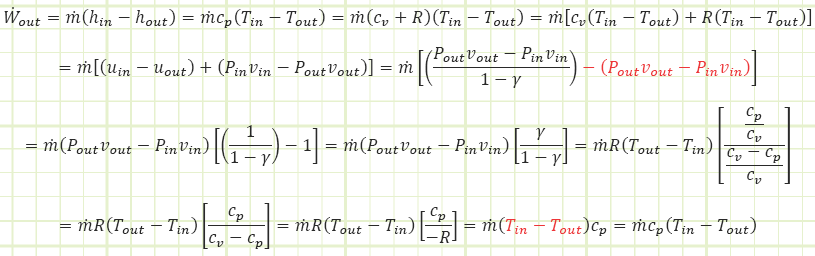Analysis of Open Systems Thermodynamics Class 7

Related Resources: thermodynamics

Analysis of Open Systems Thermodynamics Class 7

Thermodynamics Data, Equations, Charts, Equations and Calculators

Analysis of Open Systems - Class 7

Objective(s):

At the completion of the lecture, students should:

1) Be able to analyze a system when mass can cross its boundary.

2) Identify when a system is at steady state such that its material derivatives are zero.

3) Identify when a system is undergoing an unsteady process during which transfer phenomena occur.

Terminology:

Steady State: When the system is not actively increasing the amount of mass or energy stored within. Just as much energy is leaving as is entering and just as much mass is leaving as is entering, keep the material derivatives DE/Dt and Dm/Dt both equal to zero.

Consider a jet engine that has been running for a long time at a constant throttle setting. Ambient air is being ingested at the front and fuel is being injected for combustion while combustion products are exiting out the back at the same rate as air and fuel are being introduced; the mass within the system is staying constant. Meanwhile, energy is entering with the ingested air (as enthalpy) and fuel (as chemical potential energy and enthalpy, which are often just modeled as a simple heat addition) and energy is being blown out the back with the hot combustion products and also extracted as useful shaft work; however, the amount of energy inside the control volume is not changing because just as much is leaving as is coming in.

Unsteady: When the system accumulates or discharges mass, energy, or both as it experiences a process (or series of processes) from an initial state to a final state.

Consider a spent SCUBA tank being charged with pressurized air. The amount of stored mass increases as well its stored energy.

Consider a bathtub half full of saturated liquid water that then receives a block of ice below the freezing temperature of water. After enough time the system will reach a new equilibrium temperature. The amount of mass has increased (as a result of the ice addition) and the total stored energy has also increased (because even cold ice has energy); however, the specific energy has probably decreased relative to what it was prior to the ice being introduced.

Key Ideas:

What does the Equation Look Like for the conservation of mass?

The general equation for the conservation of mass as a rate-based differential equation:

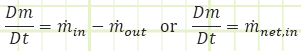
general equation for the conservation of mass

The rate of change of the amount of mass stored in the system equals the net inflow of mass to the system. If the system is at steady state, then the Dm/Dt term is equal to zero, meaning just as much mas leaves as enters. For an unsteady process:

If the mass flow rates were constant (or nearly constant) over the increment of time studied, Δt, the above unsteady equation could have been derived from the steady equation:

What does the Equation Look Like for the conservation of energy?

The general equation for the conservation of mass as a rate-based differential equation:

general equation for the conservation of mass as a rate-based differential equation

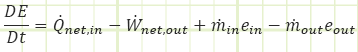
The rate of change of the amount of energy stored in the system equals the net inflow of mass-carried energy (ke, pe, Pv, and u) to the system. If the system is at steady state, then the DE/Dt term is equal to zero, meaning just as much mas leaves as enters.

Since we’re in thermo and usually thermal energy is the only type of energy of concern, we often consider ke and pe to be insignificant. Sometimes ke is significant, though! Jet engines! Nozzles! Diffusers! Dense fluids! That last one could also make pe significant if there’s an appreciable elevation change.

pe significant if there’s an appreciable elevation change

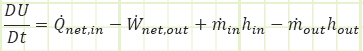
For an unsteady process that took place over some amount of time, we relate the final and initial states via:

unsteady process that took place over some amount of time,

Or for thermal energy conservation only:

thermal energy conservation only

If the mass flow rates were constant (or nearly constant) over the increment of time studied, Δt, the above unsteady equation could have been derived from the steady equation:

Remember that enthalpy is just the sum of the internal energy and the pressure energy (sometimes called flow energy or even flow work) seen in the Bernoulli equation.

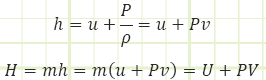
enthalpy is just the sum of the internal energy and the pressure energy

Or, as a time rate:

Notes on ṁ

What’s the velocity profile look like within a pipe or duct? Short answer: it’s generally not uniform but is a function of distance away from the interior surfaces of the wall(s). It’s max in the center, zero at the wall(s).

velocity profile look like within a pipe or duct

So we work with the mean velocity:

work with the mean velocity

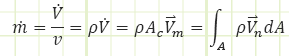
Quick example of velocity, volumetric flow rate, and mass flow rate

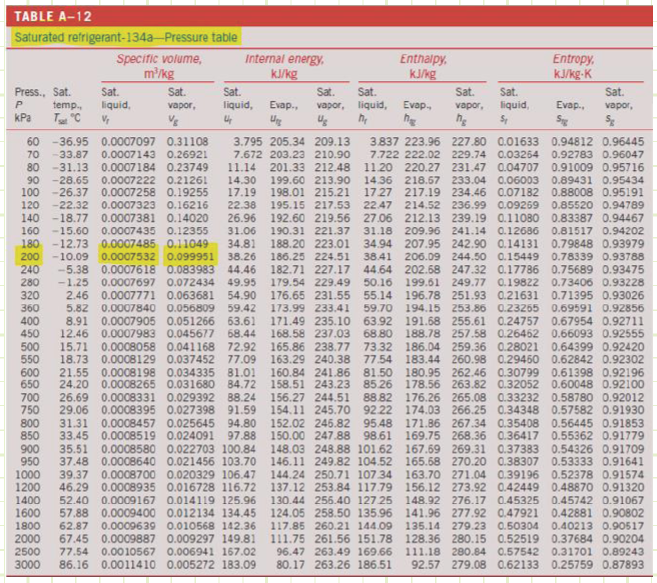
Refrigerant-134a at 200 kPa and 40% quality, flows through a 1.1-cm inside diameter, D_i, tube with an average velocity of 50 m/s. Find the mass flow rate of the refrigerant-134a.

Step 1: At P = 200 kPa and x = 0.4 we determine the specific volume using the following Table A-12:

How much energy does the flow have at some arbitrary unchanging elevation?

The kinetic energy only accounts for 1.02% of the total energy of the flowing fluid.

What is the relative contribution each form of energy offers to the total energy?

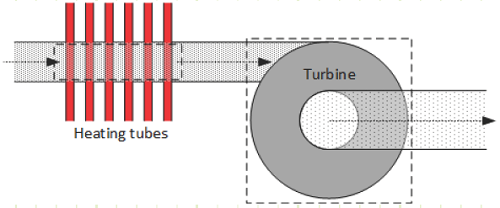
EXAMPLE 1 – STEADY FLOW ISOBARIC HEATING FOLLOWED BY ADIABATIC EXPANSION IN A WORK PRODUCING TURBINE

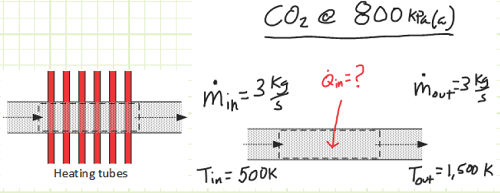
The diagram above depicts two components used in a power-producing device using carbon dioxide, CO₂, with rigid control volumes indicated around each. Gaseous CO₂ at 500 K and 800 kPa(a) enters a heat exchanger at a steady rate of 3 kg/s where it is isobarically heated to 1,500 K.

a. Determine the heat transfer [kW] required to perform this operation.

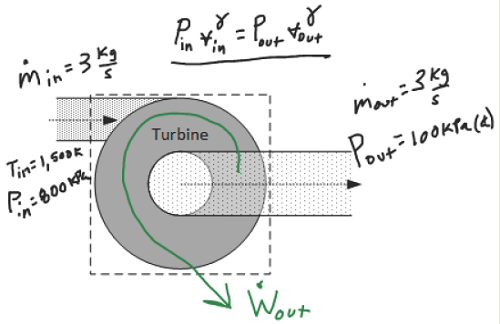
The heated CO2 then enters an ideal turbine in which it adiabatically expands until its exit pressure is 100 kPa(a).

b. Determine the temperature [K] of the methane as it exits the turbine.

Analysis:

Part a)

We can apply the First Law to the control volume.

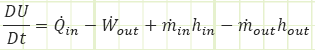
Part b)

How can we find temperature? Perhaps a couple of possibilities: First Law or Ideal Gas Equation of State. Looking at First Law:

Except we don’t actually know W_out for this steady flow operation, yet. Perhaps we can find it. Before we try that, let’s visit the Ideal Gas Equation of State.

Ideal Gas Equation of State

Okay, so we don’t have V_out, but we DO have a polytropic relationship relating P and v at the end of the process to what they were at the beginning of the process.

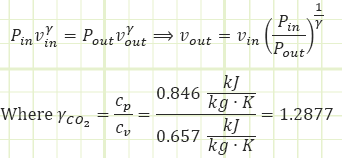
polytropic relationship relating P and v at the end of the process

But we don’t have V_in. Can we find it? Well, we DO know P_in and T_in just prior to the turbine, so the Ideal Gas equation can be of assistance:

Applying this to our adiabatic process equation to find V_out coming out of the turbine:

Now we can use the ideal gas equation of state to find T_in:

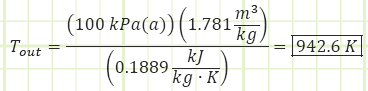
ideal gas equation of state to find T

Revisiting the First Law equation, let’s see if we can verify our answer. Can the boundary work equation we’ve typically used for unsteady closed processes apply to this steady flow open system?

Let’s plug this into our First Law formula to see if it spits out the value of T_out that we’ve already calculated:

Absolutely not. It would appear our attempt to verify the result by another avenue actually shows we can’t use the boundary work equation we’ve been applying to closed unsteady processes to this open steady flow process. Why? Because there’s FLOW WORK being performed, Pv.

Looking at it again:

Can also be written as:

That boundary work equation? Well, it’s only part of this adiabatic story. Namely, this part: u_in - u_out, so:

Okay, so there’s that number again. But what about the Pv terms?

So it would appear the turbine is also extracting power from the flow energy (a.k.a. pressure energy) as the CO₂ expands. The total power from these two enthalpic interactions is:

Is this how much power our turbine is extracting? Let’s use the First Law, solving for W_out to verify:

Voilà! We have verification. What did we learn? The equation for the calculation of boundary work for a closed system only accounts for part of the overall steady flow work story. Sure, the expansion of the gas in the turbine DOEs contribute a lot to the work output, but we also need to account for the Pv components that are inherent of a flow regime. Looking at our adiabatic First Law equation one more time and applying the ideal gas identify, c_p = c_v + R , we can see the connection:

And we go around and around and around, but ultimately we were able to manipulate the heck out of it using identities involving specific heat capacities and the specific gas constant to basically show ourselves why the flow energy terms are important in addition to the adiabatic boundary work term.

Source

Unknown Contributor - Reddit