Ideal Gas Assumptions Class 02

Related Resources: thermodynamics

Ideal Gas Assumptions Class 02

Class 2 – Ideal Gas Assumptions, Properties of Pure Substances, & Property Tables

Objective(s):

At the completion of the lecture, students should:

1) Identify when it is reasonable to use the ideal gas equation of state.

2) Identify when use of the Ideal Gas Equation is not warranted.

3) Locate and use the Property Tables in the appendix for superheated steam and refrigerant to obtain properties of interest for a given state.

4) Know about the NIST Chemistry WebBook and how it can be used to generate property tables for many more substances.

Methodology:

Asynchronous video lecture w/ OneNote. and video (Triple Point , Critical Point , Steam Power 1 , Steam Power 2 , Steam Turbines ).

Terminology:

System: A place in space with a defined boundary, within which we care about the properties of its contents. Your body is a system that interacts with the surroundings by various transport phenomena, like eating, breathing, perspiring, getting cold, lifting/pushing/pulling, being warmed by sunlight etc.

Surroundings: Everything outside of the system. Generally, we don’t care about its mass, although its temperature and pressure could be very important.

Continuum: the concept that although a system is made of distinct individual constituents, they’re so small and close together (there are roughly 10¹⁶ air molecules in a cubic millimeter of this room’s air!) that we don’t have to worry much about spatial differences between the molecules and treat it all as a smeared entity in which the properties are uniform throughout.

Pure substance: A compositionally homogenous system. If all of one chemical compound, it’s pure, even if it’s present in multiple phases. If a mixture of multiple chemical compounds (like air as a mixture of N₂ & O₂), they need to be isotropically distributed (can’t have localized concentrations of one compound surrounded by another; the constituents of air are all mixed up and in the same phase).

Property: A characteristic of a system’s contents, such as pressure, temperature, volume, internal energy, etc. Can be independent of mass (pressure & temperature), which makes it an intensive property. An extensive property depends on the amount of substance there is (total energy, total volume). If we divide out the amount of mass, it becomes a specific quantity, such as m³/kg (i.e. specific volume, which is the inverse of density).

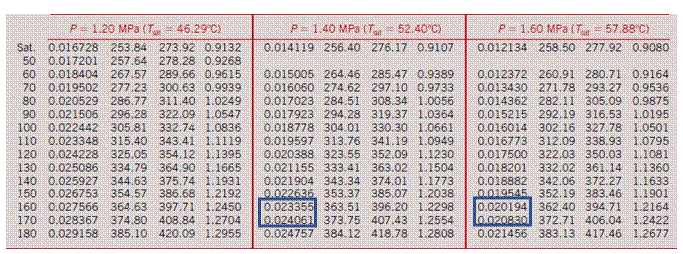
State: a stable condition in which a system is everywhere homogenous (isotropic) and therefore in equilibrium with itself. For simple compressible systems, knowing two intensive or specific properties completely specifies the overall state from which all the other intensive and specific properties can be determined. States describe a single point location on the overall 3D surface of all available states (see Lecture 2 for the Ideal Gas P-v-T surface).

Process: Something that causes a system’s state to change to a different state in which properties have changed. Thermodynamic processes are idealized as being done VERY slowly in order for every infinitesimally different intermediate state to be in equilibrium with itself. Heating, cooling, compressing, expanding, adding/subtracting mass, chemically reacting, lifting/dropping, accelerating, etc. are all processes that change the state of a system by following a certain path along the surface of available states.

Equilibrium: When a system contains no unbalanced potentials (or driving forces). If left alone, the properties of the system won’t change with regard to time or location. Equilibrium takes several forms: Thermal – the temperature is the same throughout the system. Mechanical – no unbalanced differences in pressure at any points in system (for liquid, static head induced pressure would not change for any given depth). Chemical – no chemical reactions; chemical composition remains constant.

Quasi-Equilibrium process: When a system undergoes a process so slowly that there are no significant gradients in property values. The entire control volume has sufficient time to “catch up” and absorb the total effect of whatever just changed (a moving boundary, an addition of heat in a particular location, total dispersal of injected mass, etc.)

Phase: when a substance is physically identified as having a distinct molecular arrangement that is homogenous throughout and separated from other by easily identifiable boundary surfaces (typical phases are solids [i.e.] harder, don’t flow, distinct shape], liquid [flow in the presence of a shearing force, molecules are close together, adopt whatever shape contains them, exhibit surface tension], and gases [flow easily, compressible]).

Saturated vapor: When a vapor is about to condense if any heat is removed (at constant pressure) or if pressure is increased (at constant temperature) or if volume is reduced (and heat is removed), otherwise it will become superheated.

Superheated vapor: A vapor that is not about to condense. Adding heat raises it temperature (at constant pressure), removing heat lowers its temperature (again, at constant pressure).

We Love The Ideal Gas Equation! Except when we can’t use it.

Due to the very simplistic assumptions (i.e. Newton’s Second Law, atoms are perfectly elastic bouncy balls with insignificant atomic volume) we made to derive the ideal gas equation of state, the theory falls apart outside its area of applicability because:

1) There are actually cohesive forces between molecules.

2) The molecules themselves start taking up appreciable volume within the container.

3) Multi-atom compounds can store energy by rotating and vibrating in addition to translating.

So, using the ideal gas law for low-pressure, low-density, high-temperature gases works fairly well. It works less well for dense or cold gaseous systems. It can be pretty terrible for water or refrigerant vapor, but there are tables available. Monoatomic gases fit the model quite well, multi-atomic gases lesser so, but still pretty well at high-temperature, low density, and low-pressure (which are all relative for each specific substance).

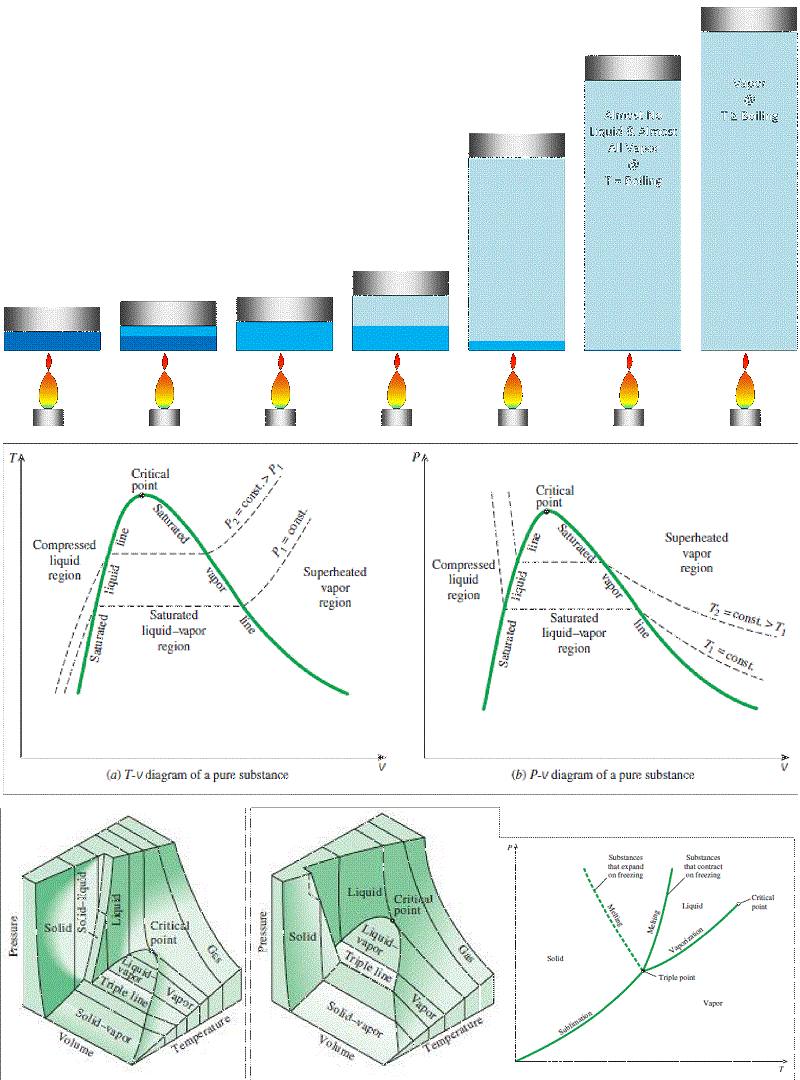
Phase Change:

Isobaric (constant pressure) heating of a pure substance from frozen solid to superheated vapor:

So what do these diagrams tell us about water? Can it ever be modeled as an ideal gas? Yes!

Where the properties are sufficiently far from the critical point or higher-pressure condensation line, it’s actually pretty OK to use the Ideal Gas Equation of State to model water vapor (or steam) as an ideal gas with R = 0.4615 kJ/kg·K

This will be VERY useful to us at the end of the class when we introduce the concept of humidity and psychrometrics.

But what about those times when we’re NOT in the shaded region of that diagram? What if my temperature and pressure are 300°C and 1,000 kPa, respectively? What will my density of my superheated steam be if I try to use the ideal gas correlation?

ρ = P / RT = 1,000 kPa / [ ( 0.4615 ( kPa · m³ / kg · K ) ( 573.15 K ) ]

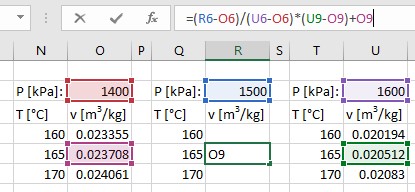
How does this compare with the true value? Well, we don’t have an easy-to-apply-in-one-easy-step equation. Instead, some really smart people developed some differential equations that relate water’s properties to its other properties (ones that can be easily measured). In doing so, tables were produced. Let’s take a look at Appendix A-6:

This table describes a (small) portion of the multidimensional surface of all available states for water when it’s in the superheated region. In addition to the properties we’ve met so far (P, v, T), we’re also seeing some other properties that will be relevant to us soon (u [Specific Internal Energy – think molecular collisions], h [Specific Enthalpy, which is just u + Pv], and s [Specific Entropy, this is how smeared-out the Boltzmann Distribution is {i.e. how unsure we are of being able to accurately predict the speed and position of a given molecule in a population of many molecules}]).

What can this table tell us about steam at 300°C and 1 MPa? Well, the exact value of specific volume is provided for these two properties. It is 0.25799 m³/kg. Taking its inverse to obtain density, we see that one cubic meter of this steam will have a mass of 3.876 kg/m³. Our ideal gas equation gave us a value that was inaccurate by a factor of 2.6%. Maybe that’s not actually so bad, but why sacrifice accuracy when it was actually easier to just look up the value?

What if we’re at 1 MPa and 315°C? Well, we can linearly interpolate between known values.

A quick mental check shows that this value is in-between the two values associated with 300°C and 350°C, respectively. If it weren’t, then there’s a mistake in the calculation somewhere.

What if it’s at 300°C and 1.08 MPa? Well, then you need to interpolate between the two known pressures, namely 1.00 and 1.20 MPa at a value of 300°C. This is still single-step interpolation between 0.21386 m³/kg (associated w/ 300°C & 1.20 MPa) and 0.25799 m³/kg (associated w/ 300°C & 1.00 MPa).

Finally, what if it’s 315°C and 1.08 MPa? This is a state with tabulated properties entirely missing from the table. It’s in-between 300&350°C and 1.00&1.20 MPa. So, you’ll need to interpolate twice, one for temperature and once for pressure. Is the end result the same with a temperature-then-pressure double interpolation as it would be for a pressure-then-temperature double interpolation. In general, you won’t calculate the exact same value, which is due to not having enough significant figures provided in the table. Personally, I would probably interpolate between temperatures first and then between pressure second…but that’s just me. You do you.

There are also tables for air! Feel free to use them (they’re actually more accurate than the ideal gas equation of state), but just know that for the exam and homework questions I’ll be assigning, I will have done my own solutions using the ideal gas equation of state (for air and other gases).

EXAMPLE 1 SPECIFIC VOLUME OF R-134A

Problem statement: I really want to know what the specific volume of R-134a refrigerant is at a temperature of 165°C and 1.5 MPa.

Given:

Substance: Refrigerant R-134a at 165°C & 1.5 MPa.

Find:

Specific volume of R-134a at the given temperature and pressure.

Assumptions:

1) For part (a), assume it is an ideal gas with R = 0.08149 kPa-m³ / kg · K

2) For Part (b), assume it is not an ideal gas.

3) Assume R-134a is a simple compressible substance for which two known properties will define the entire state, unless it turns out it’s a saturated mixture.

4) Given pressure is the thermodynamic absolute pressure.

Solution:

a) Use the ideal gas law to predict the value of specific volume:

v = RT / P = ( 0.08149 kPa-m³ / kg · K ) ( 438.15K ) / 1,500 kPa = 0.0238 m³ / kg

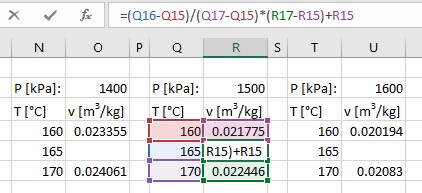
We are between known states with regard to both temperature and pressure. Time for double interpolation:

Going with a T-then-P double interpolation first:

Last step is to now interpolate between these two interpolated values using Pressure as the reference:

Honestly, it’s just way easier to do in Excel:

P [kPa]:		1400	P [kPa]:	1500	P [kPa]:	1600
T [°C]		v [m³/kg]	T [°C]	v [m³/kg]	T [°C]	v [m³/kg]
	160	0.023355	160		160	0.020194
	165	0.023708	165	0.02211	165	0.020512
	170	0.024061	170		170	0.02083

How erroneous was the Ideal Gas Equation? It was off by a factor of 7.64%. YUCK!

Okay, so how much different is our double-interpolated value if we instead approached it from a Pressure-then Temperature method?

Well, it turned out to be the exact same value. That’s a good thing! Sometimes, though, I believe I’ve found it doesn’t work out that way; although maybe I’m remembering it wrong and maybe it is actually always the same thing. Bottom line, it shouldn’t much matter in which order you choose to interpolate.

P [kPa]:	1400	P [kPa]:	1500	P [kPa]:	1600
T [°C]	v [m³/kg]	T [°C]	v [m³/kg]	T [°C]	v [m³/kg]
160	0.023355	160	0.021775	160	0.020194
165		165	0.022110	165
170	0.024061	170	0.022446	170	0.02083

Discussion:

The appendices of the textbook have a lot of great information and you’ll be expected to navigate it efficiently during exams.

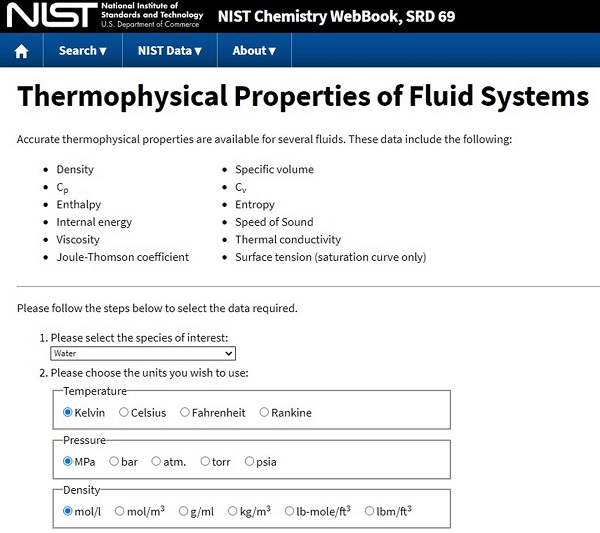
Sometimes, however, you may be asked about a substance NOT contained within the appendices. For these instances, you can either go out and buy a really big, expensive chemistry reference manual or go to the NIST Chemistry WebBook at which you can generate you own property tables for MANY common working fluids.

It takes a little practice to get it set up quickly, but once you understand the interface, it can be an incredibly powerful tool.

Source

Unknown Contributor - Reddit