Related Resources: fluid flow

Pitot Tube Theory and Application

Pitot Tube Theory and Application

This instrument is very important in aviation to calculate the speed of airplanes with respect to the air.

The animation below shows an airplane Pitot tube and the relationship between its speed and the height of the second tube.

This relationship is explained by the Bernoulli equation:

P 1 ρ ⋅ g + z 1 + V 1 2 2 g = P 2 ρ ⋅ g + z 2 + V 2 2 2 g

The equation in this case means that at two different points (1 and 2) of a runoff, the total energy remains constant,

This energy consists of the potential energy due to head (z), flow velocity (v) and pressure (P).

Points (1) and (2) are taken according to the following figure:

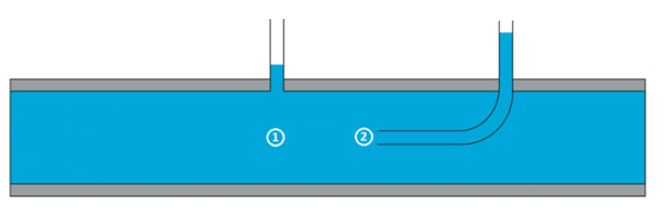
At point (1) and (2) the head z is the same, while at point (2) the flow velocity is 0, so the equation reduces to:

P 1 ρ ⋅ g + V 1 2 2 g = P 2 ρ ⋅ g

To obtain the pressures in (1) and (2), the height of the fluid in the respective tubes is measured, according to the figure:

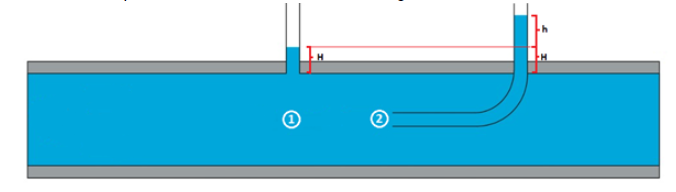
The hydrostatic pressure is calculated at both points:

Hydrostatic pressure:

P = ρ ⋅ h ⋅ g

On point (1):

P 1 = ρ ⋅ g ⋅ H ρ ⋅ g = H

At point 2:

P 2 = ρ ⋅ g ⋅ ( H + h ) ρ ⋅ g = H + h

With which the equation remains:

H + V 1 2 2 g = H + h V 1 2 2 g = h

It is in this expression where we can see that the increase in measurement height is due to the kinetic energy at point 2 of the fluid.

This energy is transformed into pressure as it travels through the tube and causes the fluid to rise in h. Finally, we clear ν 1 :

V 1 = 2 g h

As you can see, the calculation of the velocity does not depend on the density of the fluid or its specific weight, only the height h of the tube (2).

Related:

Link to this Webpage:

Copy Text to clipboard

Spider Optimizer

© Copyright 2000 - 2024, by Engineers Edge, LLC
www.engineersedge.com
All rights reserved
Disclaimer | Feedback
Advertising | Contact