| RECTANGULAR CONCRETE BEAM/SECTION ANALYSIS |
| Flexure, Shear, Crack Control, and Inertia for Singly or Doubly Reinforced Sections |
| Per ACI 318-05 Code |
| Hover Curser over Results Value to See Notes |
|
|
|
|
|
|
|
|
|
|
| Input Data: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
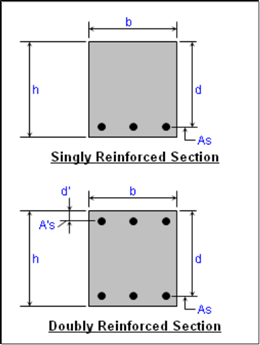 |
|
|
|
|
| Beam or Slab Section? |
|
|
|
|
|
|
|
| Exterior or Interior Exposure? |
|
|
|
|
|
|
|
| Reinforcing Yield Strength, fy = |
|
ksi |
|
|
|
|
|
| Concrete Comp. Strength, f 'c = |
|
ksi |
|
|
|
|
|
| |
|
in. |
|
|
|
|
|
| Depth to Tension Reinforcing, d = |
|
in. |
|
|
|
|
|
| |
|
in. |
|
|
|
|
|
| Tension Reinforcing, As = |
|
in.^2 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Tension Reinf. Bar Spacing, s1 = |
|
in. |
|
|
|
|
|
| Clear Cover to Tension Reinf., Cc = |
|
in. |
|
|
|
|
|
| Depth to Compression Reinf., d' = |
|
in. |
|
|
|
|
|
| Compression Reinforcing, A's = |
|
in.^2 |
|
|
|
|
|
| Working Stress Moment, Ma = |
|
ft-kips |
|
|
|
|
|
| Ultimate Design Moment, Mu = |
|
ft-kips |
|
|
|
|
|
| Ultimate Design Shear, Vu = |
|
kips |
|
|
|
|
|
| Total Stirrup Area, Av(stirrup) = |
|
in.^2 |
|
|
|
|
|
| Tie/Stirrup Spacing, s2 = |
|
in. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Results: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
Crack Control (Distribution of Reinf.): |
|
| b1 = |
|
|
|
|
?? Per ACI 318-05 Code: |
|
| c = |
|
in. |
|
|
Es = |
|
ksi |
|
| a = |
|
in. |
|
|
Ec = |
|
ksi |
|
| rb =?? |
|
|
|
|
n = |
|
n = Es/Ec |
|
| r(prov) =?? |
|
|
|
|
fs = |
|
ksi |
|
| r(min) =?? |
|
|
|
|
fs(used) = |
|
ksi |
|
| As(min) = |
|
|
|
|
s1(max) = |
|
|
| r(temp) =?? |
|
(total for section) |
|
|
|
|
|
| As(temp) = |
|
|
|
|
?? Per ACI 318-95 Code: |
|
| r(max) =?? |
|
|
|
|
dc = |
|
in. |
|
| As(max) = |
|
|
|
z = |
|
k/in. |
|
| f 's = |
|
|
|
|
z(allow) = |
|
|
| fMn = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
Moment of Inertia for Deflection: |
|
| fVc = |
|
|
|
fr = |
|
ksi |
|
| fVs = |
|
kips |
|
|
kd = |
|
in. |
|
| fVn = fVc+fVs = |
|
|
|
|
Ig = |
|
in.^4 |
|
| fVs(max) = |
|
|
|
|
Mcr = |
|
ft-k |
|
| Av(prov) = |
|
in.^2?? = Av(stirrup) |
|
Icr = |
|
in.^4 |
|
| Av(req'd) = |
|
|
|
|
Ie = |
|
in.^4?? (for deflection) |
|
| Av(min) = |
|
|
|
|
|
|
|
|
| s2(max) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
c = |
|
in. |
|
|
|
|
|
|
|
a = |
|
in. |
|
|
|
|
|
|
|
r =?? |
|
|
|
|
|
|
|
|
|
As = |
|
in.^2 |
|
|
|
|
|
|
|
(4/3)*As = |
|
in.^2 |
|
|
|
|
|
|
|
f 's = |
|
ksi |
|
|
|
|
|
|
|
A's = |
|
in.^2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|