Related Resources: calculators

Concentrated Moment Left Vertical Member 8 Deflections Equation and Calculator

Beam Deflection and Stress Equation and Calculators

Reaction and deflection formulas for in-plane loading of elastic frame.

Concentrated Moment on the Left Vertical Member Elastic Frame Deflection Left Vertical Member Guided Horizontally, Right End Pinned Equation and Calculator.

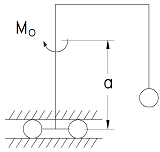
Loading Configuration

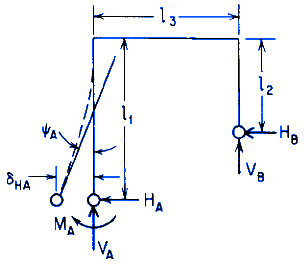
General Designations

ALL calculators require a Premium Membership

Preview

Frame Deflections with Concentrated Moment Calculator:

Since ψ_A = 0 and H_A = 0

M_A = LP_M / A_MM = Moment (Couple) at Left Node A

δ_HA = A_HM M_A - LP_H = Horizontal Deflection at Left Node A

Where:

Loading Terms LP_H and LP_M are given below.
Reaction loads and moments V_A and V_B, and H_B can be evaluated from equilibrium equations after calculating H_A and M_A.

Note: Δ_o could also be an increase in the length l₁ or a decrease in the length l₂.

Where:

Δ_o = Displacement (in, mm),
θ_o = Angular Displacement (radians),
W = Load or Force (lbsf, N),
w = Unit Load or force per unit length (lbs/in², N/mm²),
M_A = Couple (moment) ( lbs-in, N-mm),
M_o = Couple (moment) ( lbs-in, N-mm),
θ_o = Externally created angular displacement (radians),
Δ_o, = Externally created concentrated lateral displacement (in, mm),
T₁ - T₂ = Uniform temperature rise (°F),
T_o = Average Temperature (deg °F),
γ = Temperature coefficient of expansion [ µinch/(in. °F), µmm/(mm. °F) ],
T₁, T₂ = Temperature on outside and inside respectively (degrees),
H_A, H_B = Horizontal end reaction moments at the left and right, respectively, and are positive clockwise (lbs, N),
I₁, I₂, and I₃ = Respective area moments of inertia for bending in the plane of the frame for the three members (in⁴, mm⁴),
E₁, E₂, and E₃ = Respective moduli of elasticity (lb/in², Pa) Related: Modulus of Elasticity, Yield Strength;
γ1, γ2, and γ3 = Respective temperature coefficients of expansions unit strain per. degree ( in/in/°F, mm/mm/°C),
l₁, l₂, l₃ = Member lengths respectively (in, mm),

References:

Roark's Formulas for Stress and Strain, Seventh Edition